Foundations of Natural Language Processing - Lecture Notes

Table of Contents

14 January 2020

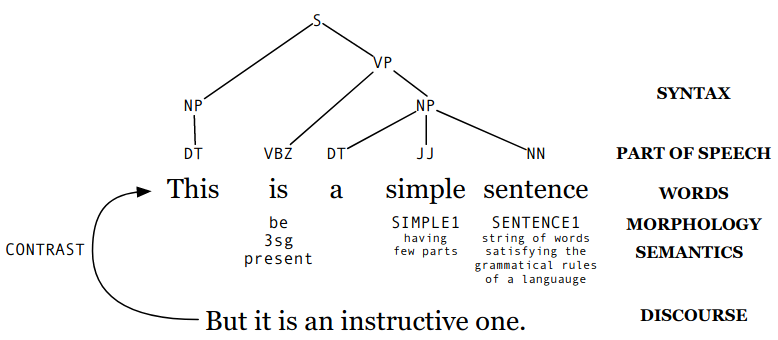
• Syntax, Part of Speech, Words, Morphology, Semantics, and Discourse

  

• Why NLP is hard?

  • Because there ambiguity at many levels:

    1. Word senses: “bank” (finance or river?)
    2. Part of Speech: “chair” (noun or verb?)
    3. Syntactic structure: “I saw a man with a telescope” (did you use a telescope to saw the man or did the man have a telescope?)
    4. Quantifier scope: “Every child loves some movie” (there exist a movie that every child loves or every child loves at least one movie)
    5. Multiple: “I saw her duck” (you saw her ducking or you saw a duck that she had)
    6. Reference: “John dropped the goblet onto the glass table and it broke” (what broke?)
    7. Discourse: “The meeting is cancelled. Nicholas isn’t coming to the office today.” (is the meeting cancelled because he isn’t coming or is he not coming because the meeting is cancelled?)

• There are two ways of dealing with ambiguity:

  • Non-probabilistic methods, returning all possible answers

    • e.g. FSMs for morphology, CKY parsers for syntax

  • Probabilistic methods returning the best possible analysis

    • e.g. HMMs for PoS tagging, PCFGs for syntax, Viterbi, probabilistic CKY
    • The best analysis is only good if our model’s probabilities are accurate; so where do accurate probabilities com from?

• Statistical NLP

  • Like most other parts of AI, NLP today is dominated by statistical methods

  • Typically more robust than earlier rule-based methods

  • Probabilities are learned from data

    • Usually requires lots of data about any particular phenomenon

• Why NLP is hard again?

  • Zipf’s Law

    

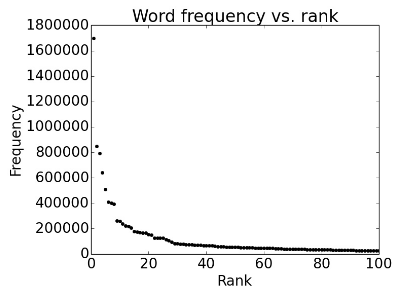
    • The frequency of a word is inversely proportional to its rank in the frequency table (and it’s also exponential!) $f \times r \approx k$

      • $f$ for frequency, $r$ for rank, and $k$ for constant
      • So that the most common word, say “the”, occurs 1m times in a corpus whereas the 20th most common word, say “do”, occurs only 200k times.

    • It’s a natural phenomenon that is observed in other languages and other fields as well.

    • Regardless of the size of your corpus!

    • Can also be observed for other linguistic structure (e.g. syntactic rules in a CFG).

    • These mean that we need to find clever ways to estimate probabilities for things we have rarely or never seen during training.

  • Variation

    • Suppose we train a Part of Speech tagger on the Wall Street Journal, which is nice and neat and copy-edited.

    • What will happen if we try to use this tagger for social media?

      ikr smh he asked fir yo last name

  • Expressivity

    • Not only can one form have different meanings (ambiguity) but the same meaning can be expressed with different forms:

      • She gave the book to Tom vs. She gave Tom the book
      • Some kids popped by vs. A few children visited
      • Is that window still open vs. Please close the window

  • Context Dependence

    • Last example also shows that the correct interpretation is context-dependent and often requires world knowledge (that the person is angry for instance)

17 January 2020

Corpora

• A corpus is a body of utterances, as words or sentences, assumed to be representative of and used for lexical, grammatical, or other linguistic analysis.

• To understand and model how language works, we need empirical evidence. Ideally, this should be naturally-occurring corpora.

• Aside from utterances, corpus datasets include metadata – side information about where the utterances come from, such as author, date, topic, publication, etc.

• Corpora with linguistic annotations are of particular interest for core NLP and therefore this course, where humans have read the text and marked categories and/or structures describing their syntax and/or meaning.

  • Can be derived automatically from the original data artifact (such as star ratings) too.
  • Consistency of human annotators is a big issue. Unambiguous rules are required to resolve disagreements.

Sentiment Analysis

• Goal predict the opinion expressed in a piece of text.

  • Either positive or negative
  • Or a rating on a scale

• The simplest way is to count the number of words with positive and negative denotations/connotations.

Building a Sentiment Analyser

1. What is the input for each prediction? Sentence? Full review text? Text + metadata?

2. What are the possible outputs? + or -? stars?

3. How will it decide?

   • When a system’s behaviour is determined solely by manual rules or databases, it is said to be rule-based, symbolic, or knowledge-driven (early days of computational linguistics)

   • Learning is the act of collecting statistics or patterns automatically from corpora to govern the system’s behaviour (dominant in most areas of contemporary NLP)

     • Supervised learning is when the data provides example input-output pairs (main focus of this course)
     • Core behaviour: training Refining behaviour: tuning

4. How will you measure its effectiveness?

The last one, at least, requires data!

• BEFORE you build a system, choose a dataset for evaluation.

• Why is data-driven evaluation is important?

  • Good science requires controlled experimentation.
  • Good engineering requires benchmarks.
  • Your intuitions about typical inputs are probably wrong.

• Often you should have multiple evaluation datasets: one for development as you hack on your system, and one reserved for FINAL testing.

  • So that we don’t optimise for the benchmark only! (for instance by overfitting)

• Gold labels: Correct labels

• Evaluation

  • Simplest measure: $\text{accuracy} = \frac{\text{# correct}}{\text{# total}}$

A Simple Sentiment Classification Algorithm

• Use a sentiment lexicon to count positive and negative words:

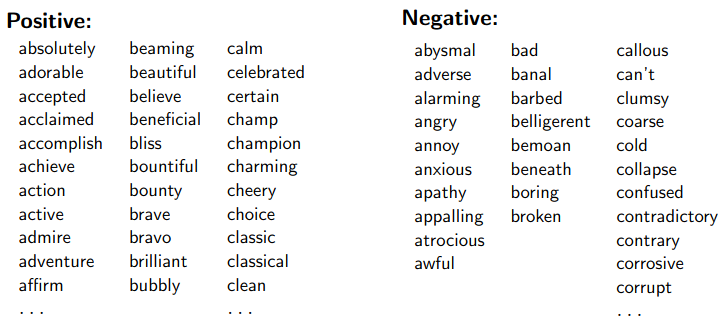
• Simplest rule: Count positive and negative words in the input. Predict whichever is greater.

• Problems:

  1. Hard to know whether words that seem positive or negative tend to actually be used that way:

     • sense ambiguity e.g. “It was awfully beautiful.”
     • sarcasm / irony e.g. “Oh yeah it was definitely wonderful!”
     • text could mention expectations or opposing viewpoints, in contrast to author’s actual opinion e.g. “I was expecting a great movie as my friends described it as a brilliant classic but I think it was just awful.”

  2. Opinion words may be describing for example a character’s attitude rather than being an evaluation of the film.

  3. Some words act as semantic modifiers of other opinion-bearing words/phrases so interpreting the full meaning requires sophistication:

     • I can’t stand this movie
     • I can’t believe how great this movie is
  • To address #1: A data-driven method: Use frequency counts from a training corpus to ascertain which words tend to be positive or negative.

Preprocessing & Normalisation

• Normal written conventions often do not reflect the “logical” organisation of textual symbols.

  • For example, some punctuation marks are written adjacent to the previous or following word, even though they are not part of it.
  • The details vary according to language and style guide even!

• Given a string of raw text, a tokeniser adds logical boundaries between separate words/punctuation tokens (occurrences) not already separated by spaces:

  

  • To a large extent, this can be automated by rules. But there are always difficult cases (e.g. “C-3PO”).

• English tokenisation conventions vary somewhat —e.g., with respect to:

  • clitics (contracted forms): ’s, n’t, ’re, etc.
  • hyphens in compounds like president-elect

• Word-level tokenisation is just part of the larger process of preprocessing or normalisation, which may also include

  • encoding conversion

  • removal of markup

  • insertion of markup

  • case conversion

  • sentence boundary detection

    • Called sentence tokenisation

• It should be evident that a large number of decisions have to be made, many of them dependent on the eventual intended use of the output, before a satisfactory preprocessor for such data can be produced.

  • Documenting those decisions and their implementation is then a key step in establishing the credibility of any subsequent experiments.

    • Documentation is especially important if the dataset is to be distributed publically.

Choice of Training & Evaluation Data

• We know that the way people use language varies considerably depending on context. Factors include

  • Mode of Communication Speech (in person, telephone, …), writing (print, SMS, Web, …)
  • Topic Chit-chat, politics, sports, physics, …
  • Genre News story, novel, Wikipedia article, persuasive essay, political address, tweet, …
  • Audience Formality, politeness, complexity (e.g. child-directed speech), …
  • In NLP, domain is a cover-term for all these factors.

• Statistical approaches typically assume that the training data and the test data are sampled from the same distribution.

  • I.e. if you saw an example data point, it would be hard to guess whether it was from the training or test data

• Things can go awry if the test data is appreciably different, e.g.

  • different tokenisation conventions
  • new vocabulary
  • longer sentences
  • more colloquial / less edited style
  • different distribution of labels

• Domain adaptation techniques attempt to correct for this assumption when something about the source/characteristics of the test data is known to be different.

21 January 2020

• Probability of a sentence is “how likely is it to occur in natural language”

  • Consider only a specific language (English) [or even British English]

  • Not including meta-language (e.g. linguistic discussion)

  • P(“the cat slept peacefully”) > P(“slept the peacefully cat”)

    • Use case: generative NLP (abstractive summarisation)

  • P(“she studies morphosyntax”) > P(“she studies more faux syntax”)

    • Use case: audio transcription

• It’s very difficult to know the true probability of an arbitrary sequence of words.

• But we can define a language model to give us good approximations.

• Like all models, language models will be good at capturing some things and less good for others.

  • We might want different models for different tasks.
  • Today, one type of language model: an n-gram model

Use Cases of a Language Model

Spelling Correction

• Sentence probabilities help decide correct spelling

Automatic Speech Recognition

• Sentence probabilities help decide between similar-sounding options.

Machine Translation

• Sentence probabilities help decide word choice and word order.

Prediction

• Language models can be used for prediction as well as correction.

• E.g. Predictive text correction/completion on your mobile phone:

  • Keyboard is tiny, easy to touch a spot slightly off from the letter you meant.
  • Want to correct such errors as you go, and lso provide possible completions.
  • Predicts as you are typing: ineff...
  • In this case, a language model may be defined over sequences of characters instead of (or in addition to) sequences of words.

Estimating Probabilities

• We want to know the probability of word sequence $\vec{w} = w_1 \ldots w_n$ occurring in English.
• Assume we have some training data: large corpus of general English text.
• We can use this data to estimate the probability of $\vec{w}$ (even if we never see it in the corpus!)

Probability Theory vs Estimation

• Probability theory can solve problems like

  • I have a jar with 6 blue marbles and 4 red ones.
  • If I choose a marble uniformly at random, what’s the probability that it’s red?

• But often we don’t know the true probabilities, only have data:

  • I have a jar of marbles
  • I repeatedly choose a marble uniformly at random and then replace it before choosing again.
  • In ten draws, I get 6 blue marbles and 4 red ones.
  • On the next draw, what’s the probability that I get a red marble?
  • First three facts are evidence.
  • The question requires estimation theory.

Notation

• $P(x)$ for true probabilities
• $\hat{P}(x)$ for estimated probabilities
• $P_E(x)$ for estimated probabilities using a particular estimation method $E$.
• But since we almost always mean estimated probabilities, we might get lazy later and use $P(x)$ for those too.

Relative Frequency Estimation

• Intuitive way to estimate discrete probabilities $P_{\text{RF}}(x) = \frac{C(x)}{N}$ where

  • $C(x)$ is the count of $x$ in a large dataset, and
  • $N = \sum_{x'}C(x')$ is the total number of items in the dataset

• This method is also known as maximum-likelihood estimation (MLE) for reasons we’ll explain.

Problems

• Using MLE on full sentences doesn’t work well for language model estimation.

  • All sentences that have never occurred get zero probability even if they are grammatical (and meaningful).

• In general, MLE thinks anything that hasn’t occurred will never occur (P=0).

  • Clearly not true! Such things can have differing and non-zero probabilities.

    • My hair turns blue.
    • I ski a black run.
    • I travel to Finland.

  • And similarly for word sequences that have never occurred.

Sparse Data

• In fact, even things that occur once or twice in our training data are a problem.
• The sparse data problem is that there are not enough observations to estimate probabilities well simply by counting observed data.
• For sentences, many (most!) will occur rarely if ever in our training data. So we need to do something far smarter.

N-Gram Models

• One way to tackle sparse data problem is to estimate $P(\vec{w})$ by combining the probabilities of smaller parts of the sentence, which will occur more frequently.
• This is the intuition behind n-gram language models.

Deriving an N-Gram Model

$\begin{align} &P(S=``\text{the cat slept quitely}'')\\ =\ &P(\text{the}, \text{cat}, \text{slept}, \text{quitely})\\ =\ &P(\text{quitely} \mid \text{the}, \text{cat}, \text{slept}) \times P(\text{the}, \text{cat}, \text{slept})\\ =\ &P(\text{quitely} \mid \text{the}, \text{cat}, \text{slept}) \times P(\text{slept} \mid \text{the}, \text{cat}) \times P(\text{the}, \text{cat})\\ \vdots \end{align}$

• More generally, we use the chain rule.

• But many of these conditional probabilities are just as sparse!

  • If we want $P(\text{the}, \text{cat}, \text{slept}, \text{quitely})$
  • We still need $P(\text{quitely} \mid \text{the}, \text{cat}, \text{slept})$

• So we make an independence assumption: the probability of a word only depends on a fixed number of previous words (called history)

  • Trigram model: $P(w_i \mid w_1, w_2, \ldots, w_{i-1}) \approx P(w_i \mid w_{i-2}, w_{i-1})$
  • Bigram model: $P(w_i \mid w_1, w_2, \ldots, w_{i-1}) \approx P(w_i \mid w_{i-1})$
  • Unigram model: $P(w_i \mid w_1, w_2, \ldots, w_{i-1}) \approx P(w_i)$

• This assumption is not always a good one! But it does reduce the sparse data problem.

• If we use MLE, we consider:

  • Out of all cases where we saw $w_{i-2}, w_{i-1}$ (in order) as the first two words of a trigram,
  • how many had $w_i$ as the third word?

Beginning/End of Sequence

• To capture behaviour at beginning/end of sequences, we can augment the input with <s> and </s>.
• Alternatively, we can model all sentences as one (very long) sequence, including punctuation.

Costs (Negative Log Probabilities)

• Word probabilities are typically very small.

• Multiplying lots of small probabilities quickly gets so tiny that we cannot represent the numbers accurately, even with double precision floating point.

• So in practice, we typically use negative log probabilities (also called costs)

  • Since probabilities range from 0 to 1, negative log probabilities range from 0 to $\infty$
  • lower cost = higher probability
  • Instead of multiplying probabilities, we add negative log probabilities

Problems

• N-gram models can be too simplistic, length of a “context” often varies: can be shorter or longer than an arbitrary $N$.

  • Longer histories may capture more but are also more sparse.

• Still suffers from assigning zero probabilities to not-seen sequences.

24 January 2020

Evaluating a Language Model

• Intuitively, a trigram model captures more context than a bigram model, so should be a “better” model.

  • That is, it should more accurately predict the probabilities of sentences.
  • But how can we measure this?

Types of Evaluation in NLP

• Extrinsic: measure performance on a downstream application

  • For a language model, plugging it into a machine translation, automated speech recognition, … system
  • The most reliable evaluation, but can be time-consuming
  • And of course, we still need an evaluation measure for the downstream system!

• Intrinsic: design a measure that is inherent to the current task

  • Can be much quicker/easier during development cycle

  • But not always easy to figure out what the right measure is

    • ideally, one that correlates well with extrinsic measures

• Let’s consider how to define an intrinsic measure for language models.

Entropy

$H(X) = \sum_x -P(x) \log_2{P(x)} = E[-\log_2P(X)]$

• Intuitively, a measure of uncertainty/disorder

  • A measure of “how surprising” a probability distribution is.

• Example: where the area of a section is proportional to its probability

  

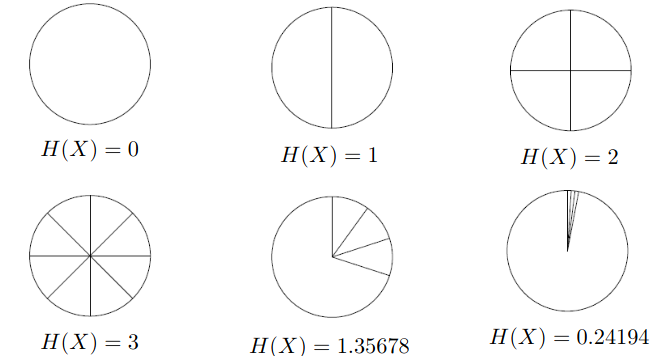
Entropy as Yes/No Questions

• Entropy is the answer to how many yes-no questions (bits) do we need to find out the outcome (or to encode the outcome)?
• Uniform distributions with $2^n$ outcomes require $n$ yes-no questions.
• Average number of bits needed to encode $X$ $\ge$ entropy of $X$

Estimates and Cross Entropy

• A good model should have low uncertainty (entropy) about what comes next.

  • Lower cross entropy means that a model is better at predicting the next element (e.g. word).

• Cross entropy measures how close $\hat{P}$ (estimate) is to $P$ (true): $H(P, \hat P) = \sum_x -P(x) \log_2\hat P(x)$

• Note that cross-entropy $\ge$ entropy

  • A model’s uncertainty can be no less than the true uncertainty.
  • But we still don’t know $P(x)$

Estimating Cross Entropy

For $w_1, \ldots, w_n$ with large $n$, per-word cross-entropy is well approximated by:

$H_M(w_1, \ldots, w_n) = -\frac 1 n \log_2 P_M(w_1, \ldots, w_n)$

• That is just the average negative log probability our model assigns to each word in the sequence (i.e. normalised for sequence length).

Perplexity

• Language model performance is often reported as perplexity rather than cross-entropy.

• Perplexity is simply $2^\text{cross-entropy}$.

  • The average branching factor at each decision point is 2, if our distribution were uniform.
  • So, 6 bits of cross-entropy means our model perplexity is $2^6 = 64$: equivalent uncertainty to a uniform distribution over 64 outcomes.

Interpreting Measures

• Cross entropy of a language model on some corpus is 5.2

• Is this good?

• No way to tell! Cross entropy depends on both the model and the corpus.

  • Some language is simply more predictable (e.g. casual speech vs academic writing)

    • So lower cross entropy could mean that the corpus is “easy”, rather than the model is good.

  • We can only compare different models on the same corpus.

    • Measured on “held-out” data.

Sparse Data, Again

• Remember that MLE assigns zero probability to never observed sequences.
• Meaning that cross-entropy would be infinite: because of $\log_2 0$
• Basically right: our model says the something should never occur, so our model is infinitely wrong (or rather, we are infinitely surprised) when it does occur!
• Even with a unigram model we will run into words we never saw before. So even with short(est) n-grams, we need better ways to estimate probabilities from sparse data.

Smoothing

• The flaw of MLE is that it estimates probabilities that make the training data maximally probable, by making everything else (i.e. unseen data) minimally probable.
• Smoothing methods address the problem by stealing probability mass from seen events and (somehow) reallocating it to unseen events.
• There are lots of different methods based on different kinds of assumptions.
• In smoothing, we have to ensure that all the probabilities still sum up to 1.

Add-One (Laplace) Smoothing

• Just pretend we saw everything one more time than we did.

$P_{+1}(w_i \mid w_{i-2}, w_{i-1}) = \dfrac{C(w_{i-2}, w_{i-1}, w_i) + 1}{C(w_{i-2}, w_{i-1}) + v}$

where $v$ is the vocabulary size.

Problems

• Laplace smoothing steals way too much from seen events.

  • In fact, MLE is pretty good for frequent events, so we shouldn’t want to change these much.

• Assumes that we know the vocabulary size in advance.

  • And also that the size of our vocabulary is fixed.
  • To remediate, we can just add a single “unknown” (UNK) item, and use this for all unknown words.

Add-α (Lidstone) Smoothing

• We can improve things by adding $\alpha < 1$

$P_{+\alpha}(w_i \mid w_{i-2}, w_{i-1}) = \dfrac{C(w_{i-2}, w_{i-1}, w_i) + \alpha}{C(w_{i-2}, w_{i-1}) + \alpha v}$

Good-Turing Smoothing

• Good is the surname of Irving John Good. :)

• Previous methods changed the denominator, which can have big effects even on frequent events.

• Good-Turing changes the numerator only.

• Think of Good-Turing like this:

  • MLE divides count $c$ of n-gram by count $n$ of history: $P_\text{ML} = \dfrac c n$
  • Good-Turing uses adjusted counts $c^*$ instead: $P_\text{GT} = \dfrac {c^*} n$

• The actual formula is skipped for brevity. I don’t think it’s actually needed.

  • Refer to 04_slides.pdf page 32 when needed.

• There are even better methods!

28 January 2020

Problems with Good-Turing

• Assumes we know the vocabulary size (i.e. no unseen words)

  • Use UNK

• Does not allow “holes” in the counts (i.e. if $N_i > 0$ then $N_{i-1}>0$)

  • Use linear regression

• Applies discounts even to high-frequency items

• Assigns equal probabilities to all unseen events

  • A better solution is to use information from lower order N-grams (shorter histories)

    • beer drinkers [likely]
    • beer eaters [unlikely]

  • Two methods:

    • interpolation
    • backoff

Interpolation

• Combine higher and lower order N-gram models, since they have different strengths and weaknesses:

  • high-order N-grams are sensitive to more context, but have sparse counts
  • low-order N-grams have limited context but robust counts

• If $P_N$ is N-gram estimate (from MLE, GT, etc; $N = 1 \text{ to } 3$), use:

  $P_\text{INT}(w_3 \mid w_1, w_2) = \lambda_1 P_1(w_3) + \lambda_2 P_2(w_3 \mid w_2) + \lambda_3P_3(w_3 \mid w_1, w_2)$

  • E.g. $P_\text{INT}(\text{three} \mid \text{I}, \text{spent}) = \lambda_1 P_1(\text{three}) + \lambda_2 P_2(\text{three} \mid \text{spent}) + \lambda_3P_3(\text{three} \mid \text{I}, \text{spent})$

• Nota bene that all $\lambda_i$s must sum to 1!

Fitting Interpolation Parameters

• In general, any weighted combination of distributions is called a mixture model.
• So $\lambda_i$s are interpolation parameters or mixture weights.
• The values of the $\lambda_i$s are chosen to optimise perplexity on a held-out dataset.

Katz Back-Off

• Solve the problem in a similar way to Good-Turing smoothing.
• Discount the trigram-based probability estimates.
• This leaves some probability mass to share among the estimates from the lower-order models.
• Instead of distributing the mass uniformly over unseen items, use it for backoff estimates
• No need to know the formula.

Diversity of Histories

• “York” almost always directly follows “New”, say in a corpus

• So, in unseen bigram contexts, York should have low probability

  • lower than predicted by unigram model as used in interpolation/backoff.

Kneser-Ney Smoothing

• Kneser-Ney smoothing takes diversity of histories into account

• Count of distinct histories for a word $N_{1+}(\cdot w_i) = |\{w_{i-1}: c(w_{i-1}, w_i) > 0\}|$

  • In the formula above, $w_{i-1}$ is the history (i.e. bigram model).

• Recall: MLE of unigram language model $P_\text{ML}(w_i) = \dfrac{C(w_i)}{\sum_w C(w)}$

• In KN smoothing, replace raw counts with count of histories: $P_\text{KN}(w_i) = \dfrac{N_{1+}(\cdot w_i)}{\sum_w N_{1+}(\cdot w)}$

• The best thing about KN smoothing is that it gives you the probability of “appearing in new contexts”

Kneser-Ney In Practice

• Original version used backoff, later “modified Kneser-Ney” introduced using interpolation.
• Fairly complex equations, but until recently the best smoothing method for word n-grams

Distributed Representations and Word Similarity

SKIPPED. See 05_slides.pdf page 19.

• E.g. Word2Vec

• Use neural networks to project words into a continuous space, so words that appear in similar contexts have similar representation.

• Can $P(\text{salmon} \mid \text{caught}, \text{two})$ tell us anything about $P(\text{swordfish}\mid \text{caught}, \text{two})$?

  • N-gram models say no.
  • But we know that both are fish and can be caught.

Noisy Channel

• We imagine that someone tries to communicate a sequence to us, but noise is introduced. We only see the output sequence

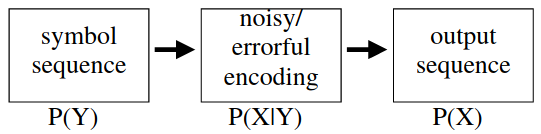
Application	Y	X
Speech Recognition	spoken words	acoustic signal
Machine Translation	words in $L_A$	words in $L_B$
Spelling Correction	intended words	typed words

• $P(Y)$ is the language model!
• $P(X \mid Y)$ is the distribution describing the “likelihood” of the output given the intention. We call it the noise model.
• $P(X)$ is the resulting distribution over what we actually see.
• Given some particular observation $x$, we want to recover the most probable $y$ that was intended.

Noisy Channel as Probabilistic Inference

• Mathematically, what we want is $\arg\max_y P(y \mid x)$

• Rewrite using Bayes’ Rule: $\begin{align}\arg\max_y P(y\mid x) &= \arg\max_y \dfrac{P(x\mid y)P(y)}{P(x)}\\ &= \arg\max_y P(x\mid y)P(y) \end{align}$

  • $P(x\mid y)$ is the noise model

    • varies heavily depending on the application: acoustic model, translation model, misspelling model, …

  • $P(y)$ is the language model

    • fairly same for different applications

• Training conditional probabilities requires input/output pairs which are often limited:

  • Misspelled words with their corrections, transcribed speech, translated text, …

• But language models can be trained on huge unannotated corpora: a better model! Can help improve overall performance.

• Assume we have a way to compute $P(x\mid y)$ and $P(y)$. Can we do the following:

  • Consider all possible intended words $y$.
  • For each $y$, compute $P(x\mid y)P(y)$.
  • Return the $y$ with highest $P(x\mid y)P(y)$ value.
  • No! Without constraints, there are (nearly) infinite number of possible $y$s.

31 January 2020

Edit Distance

• The task: find the optimal character alignment between two words (the one with the fewest character changes: the minimum edit distance or MED).

• Example: if all changes count equally, MED(stall, table) is 3:

  S T A L L
    T A L L		deletion
    T A B L   	substitution
    T A B L E		insertion
  

  • Written as an alignment:

    S T A L L -
    d | | s | i
    - T A B L E
    

• There may be multiple best alignments

  • And lots of non-optimal alignments.

• For now, all costs are equal: cost(ins) = cost(del) = cost(sub) = 1

  • But we can choose whatever costs we want! They can even depend on the particular characters involved.

Finding an Optimal Alignment

• Brute force doesn’t scale well.

  • The number of alignments to check grows exponentially with the length of the sequences.

• Instead we will use dynamic programming algorithm.

  • Strings of length $n$ and $m$ require $O(mn)$ time and $O(mn)$ space.

Chart

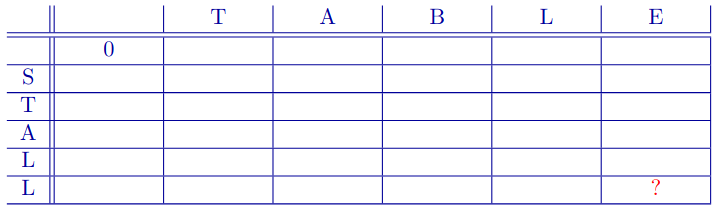
• $\text{Chart}[i, j]$ stores two things:

  • $D(\text{stall}[0..i], \text{table}[0..j])$: the MED of substrings of length $i$, $j$

    • (row, column) addressing

  • Backpointer(s): which sub-alignment(s) used to create this one.

• The Idea

  • Deletion move down

  • Insertion move right

  • Substitution move down and right

    • If the letters are identical, it’s called Identical and often has no cost.

  • Sum costs as we expand out from cell (0, 0) to populate the entire matrix.

Filling First Cell

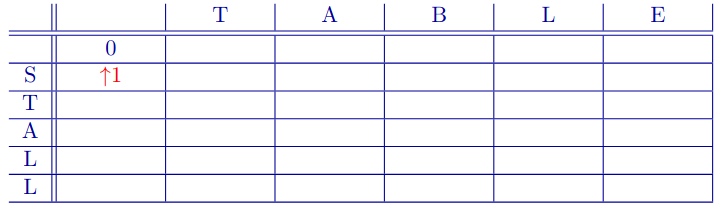
• Moving down in chart means that we had a deletion of S.

  • That is, we aligned (S) with (-).

• Add cost of deletion (1) and backpointer (to where we came from).

Second Column

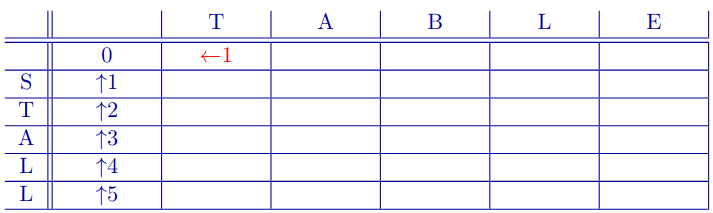
• Moving right in chart (from (0,0)) means that we had an insertion of T.

  • That is, we aligned (-) with (T).

• Add cost of insertion (1) and backpointer (to where we came from).

Single Best Path

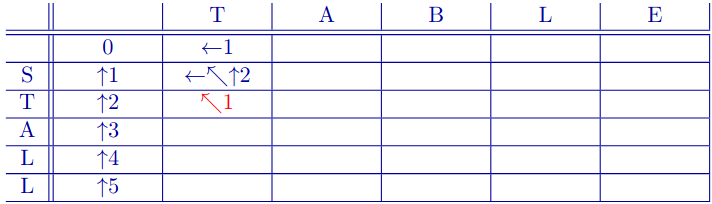
• Now compute $D(\text{ST}, \text{T})$. Take the minimum of three possibilities:

  • $D(\text{ST}, \text{-}) + \text{cost}(\text{ins}) = 2 + 1 = 3$

    • moving right from (2,0)

  • $D(\text{S}, \text{T}) + \text{cost}(\text{del}) = 2 + 1 = 3$

    • moving down from (1,1)

  • $D(\text{S}, \text{-}) + \text{cost}(\text{ident}) = 1 + 0 = 1$

    • moving down and right from (1,0), but since the letters are identical (T), it is not substitution but identical, the cost is 0

Completed Chart

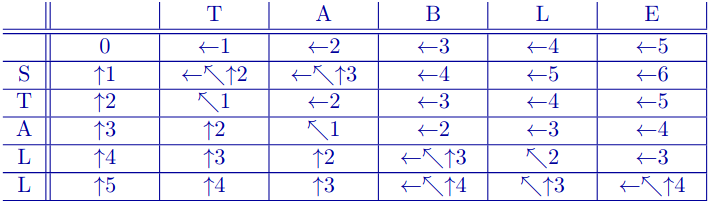
• You can enumerate all the optimum MEDs by starting from the bottom right cell and following the arrows until the top left cell.

  • If there are multiple arrows in a cell, it means that there are multiple optimum solutions.

Uses of Alignment and MED

• Computing distances and/or alignments between arbitrary strings can be used for:

  • Spelling correction

  • Morphological analysis

    • which words are likely to be related?

  • Other fields entirely

    • e.g. comparing DNA sequences in biology

  • Related algorithms are also used in speech recognition and timeseries data mining.

Catch-22

• In our examples, we used costs of 1 (insertion and deletion) and 2 (substitution) to compute alignments.
• We actually want to compute our alignments using the costs from our noise model: the most probable alignment under that model is what we are interested in.
• But alas, until we have the alignments, we can’t estimate the noise model…

General Formulation

• This sort of problem actually happens a lot in NLP (and ML).

• We have some probabilistic model and want to estimate its parameters (here, the costs).

• The model also contains variables whose value is unknown (here, the correct character alignments).

• We would be able to estimate the parameters if we knew the values of the variables…

  • … and conversely, we would be able to inter the values of the variables if we knew the values of the parameters.

Expectation-Maximisation (EM)

• Problems of this type can often be solved using a version of Expectation-Maximisation.

1. Initialise parameters to arbitrary values (e.g. set all costs to 1)

2. Using these parameters, compute optimal values for variables (run MED to get alignments).

3. Now using those alignments, recompute the parameters

   • Just pretend that alignments are hand annotations.
   • Estimate parameters as from annotated corpus.

4. Repeat steps 2 and 3 until parameters stop changing.

EM vs Hard EM

• What we have just described is actually “hard EM” (meaning: no soft/fuzzy decisions)

• Step 2 of true EM does not choose optimal values for variables, instead computes expected values.

• True EM is guaranteed converge to a local optimum of the likelihood function.

  • Hard EM also converges but not to anything nicely defined mathematically.
  • However it’s usually easier to compute and may work fine in practice.

Likelihood Function

• Let’s call the parameters of our model $\theta$.

• For any value of $\theta$, we can compute the probability of our dataset $P(\text{data}\mid\theta)$. This is the likelihood.

  • If our data includes hand-annotated character alignments, then $P(\text{data} \mid\theta) = \prod^n_{i=1}P(x_i \mid y_i)$
  • If the alignments $a$ are latent, sum over possible alignments: $P(\text{data}\mid\theta) = \sum_a\prod^n_{i=1}P(x_i\mid y_i, a)$

• The likelihood $P(\text{data}\mid\theta)$ is a function of $\theta$, and can have multiple local optima.

• Schematically (but $\theta$ is really multi-dimensional):

  

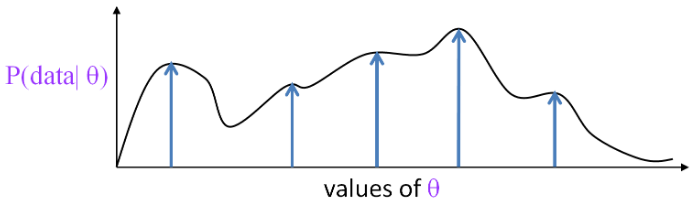
• EM will converge to one of these local optima; hard EM won’t necessarily.

• Neither is guaranteed to find the global optimum!

4 February 2020

Text Classification

• We might want to categorise the content of the text:

  • Spam detection (binary: spam or not)

  • Sentiment analysis (binary or multiway)

    • movie, restaurant, or product reviews (pos/neg, or 1-5 stars)
    • political argument (pro/con, or pro/con/neutral)

  • Topic classification (multiway: sport/finance/travel/etc)

• … or we might want to categorise the author of the text (authorship attribution)

  • Native language identification (e.g. to tailor language tutoring)
  • Diagnosis of disease (psychiatric or cognitive impairments)
  • Identification of gender, dialect, educational background, political orientation, and so on for example in forensics (legal matters), advertising/marketing, campaigning, etc.

• N-gram models can sometimes be used for classification but

  • for many tasks, sequential relationships between words are largely irrelevant: we can just consider the document as a bag of words

    • $\text{Document} \to [(\textit{word}, \text{count})]$
    • Some normalisation can be done beforehand, such as case conversion.

  • on the other hand, we may want to include other kinds of features (e.g. PoS tags) that N-gram models don’t include

• Here we consider two alternative models for classification:

  • Naive Bayes

    • Review of what we have studied last year.

  • Maximum Entropy

    • aka multinomial logistic regression

Naive Bayes

• Given document $d$ and set of categories $C$ (say, spam/not-spam), we want to assign $d$ to the most probable category $\hat c$.

$\begin{align}\hat c &= \arg\max_{c\in C} P(c \mid d)\\ &= \arg\max_{c\in C} \dfrac{P(d\mid c) P(c)}{P(d)}\\ &= \arg\max_{c\in C} P(d\mid c)P(c)\end{align}$

• Just as in spelling correction, we need to define $P(d\mid c)$ and $P(c)$.

  • $P(c)$ is the prior probability of class $c$ before observing any data.

    • Simply estimated by MLE: $\hat P(c) = \dfrac{N_c}{N}$
    • In other words, the proportion of training documents belonging to class $c$.

Modelling $P(d \mid c)$ (Feature Probabilities)

• We represent each document $d$ as the set of features (words) it contains: $f_1, f_2, \ldots, f_n$. So: $P(d\mid c) = P(f_1, f_2, \ldots, f_n \mid c)$

• As in Language Models, we cannot accurately estimate $P(f_1, f_2, \ldots, f_n \mid c)$ due to sparse data.

• So make a naive Bayes assumption: features are conditionally independent given the class: $P(f_1, f_2, \ldots, f_n \mid c) \approx P(f_1\mid c) P(f_2\mid c)\cdots P(f_n\mid c)$

• That is, the probability of word occurring depends only on the class.

  • Not on which words occurred before or after (as in N-grams)
  • Or even which other words occurred at all

• Effectively, we only care about the count of each feature in each document.

Calculating the Feature Probabilities

$P(f_i \mid c)$ is normally estimated with simple smoothing:

$\hat P(f_i \mid c) = \dfrac{\text{count}(f_i, c) + \alpha}{\sum_{f\in F}\left(\text{count}(f, c) + \alpha\right)}$

• $\text{count}(f_i, c)$ is the number of times $f_i$ occurs in class c
• $F$ is the set of possible features
• $\alpha$ is he smoothing parameter, optimised on held-out data

Alternative Features

• Use only binary values for $f_i$: did this word occur in $d$ or not?

• Use only a subset of the vocabulary for $F$

  • Ignore stopwords (function words and others with little content)

  • Choose a small task-relevant set (e.g. using a sentiment lexicon)

  • Can be tricky:

    • E.g. sentiment analysis might need domain-specific non-sentiment words: such as quiet for computer product reviews

    • And for other tasks, stopwords might be very useful features:

      • E.g. people with schizophrenia use more 2nd-person pronouns, those with depression use more 1st-person

    • Probably better to use too many irrelevant features than not enough relevant ones.

• Use more complex features (bigrams, syntactic features, morphological features, …)

Costs and Lineraity

• Multiplying large numbers of small probabilities together is problematic, thus we use costs (neg log) again.

• In which case, we look for the lowest cost overall.

• Naive Bayes then: $\hat c = \arg\min_{c\in C} \left(-\log P(c) + \sum^n_{i=1} - \log P(f_i \mid c)\right)$

• This amounts to classification using a linear function (in log space) of the input features.

  • So Naive Bayes is called a linear classifier.
  • As is Logistic Regression (to come)

Review of Naive Bayes

Advantages

• Very easy to implement
• Very fast to train, and to classify new documents (good for huge datasets)
• Doesn’t require as much training data as some other methods (good for small datasets)
• Usually works reasonably well
• This should be your baseline method for any classification task

Disadvantages

• Naive Bayes assumption is Naive.

  • Consider the following categories: travel, finance, sport

  • Are the following features independent given the category: beach, sun, ski, snow, pitch, palm, football, relax, ocean

    • No! Given travel, seeing beach makes sun more likely, but ski less likely.
    • Defining finer-grained categories might help (beach travel vs ski travel), but we usually do not want to.

  • In short, features are not usually independent given the class.

• Accuracy of classifier can sometimes still be OK, but it will be highly overconfident in its decisions.

  • For example, Naive Bayes sees 5 features that all point to class 1, and treats them as five independent sources of evidence.
  • It’s like asking 5 friends for an opinion when some got theirs from each other.

Maximum Entropy Classifiers

• Used widely in many different fields, under many different names.

  • Most commonly, multinomial logistic regression

    • multinomial if more than two possible classes
    • otherwise (or if lazy) just logistic regression

  • Also called: log-linear model, one-layer neural network, single neuron classifier, etc…

• Like Naive Bayes, Maximum Entropy assigns a document $d$ to class $\hat c$, where $\hat c = \arg\max_{c\in C} P(c\mid d)$

• Unlike Naive Bayes, Maximum Entropy does not apply Bayes’ Rule. Instead, it models $P(c \mid d)$ directly.

Features

• Like Naive Bayes, MaxEnt models use features we think will be useful for classification.

• However, features are treated differently in two models:

  • Naive Bayes

    • features are directly observed (e.g. words in doc)
    • no difference between features and data

  • Maximum Entropy

    • we will use $\vec x$ to represent the observed data.
    • features are functions that depend on both observations $\vec x$ and class $c$.

• For example, if we have three classes, our features will always come in groups of three. Imagine three binary features: $f_1:\quad \text{contains(`ski`)}\ \&\ c = 1 \\ f_2:\quad \text{contains(`ski`)}\ \&\ c = 2 \\ f_3:\quad \text{contains(`ski`)}\ \&\ c = 3$

  • N.B. the format: the “actual” feature AND class
  • training docs from class 1 that contain ski will have $f_1$ active
  • training docs from class 2 that contain ski will have $f_2$ active
  • etc.

• Each feature $f_i$ has a real-values weight $w_i$ learned in training.

Classification with MaxEnt

Choose the class that has highest probability according to

$P(c \mid \vec x) = \dfrac 1 Z \exp\left(\sum_i w_i f_i(\vec x, c)\right)$

where normalisation constant $Z = \sum_{c'} \exp\left(\sum_i w_i f_i(\vec x, c')\right)$

• Inside brackets is just a dot product: $\vec w \cdot \vec f$
• And $P(c\mid \vec x)$ is a monotonic function of this dot product.
• So, we will end up choosing the class for which $\vec w \cdot \vec f$ is highest.
• Realise that the normalisation constant $Z$ is not required for classification purposes.

Feature Templates

• In practise, features are usually defined using templates $\text{contains}(w)\ \&\ c \\ \text{header_contains}(w)\ \&\ c \\ \text{header_contains}(w)\ \&\ \text{link_in_header}\ \&\ c$
• NLP tasks often have few templates but 1,000s or 10,000s of feautres!

Training the Model

• Given annotated data, choose weights that make the labels most probable under the model.

• That is, given examples $x^{(1)}, \ldots, x^{(N)}$ with labels $c^{(1)}, \ldots, c^{(N)}$, choose $\hat w = \arg\max_{\vec w} \sum_j \log P(c^{(j)} \mid x^{(j)})$

• Called conditional maximum likelihood estimation (CMLE)

  • Like MLE, CMLE will overfit so we use tricks (regularisation) to avoid that.

Review of MaxEnt

• Supervised CMLE in MaxEnt is not so easy:

  • requires multiple iterations over the data to gradually improve weights (using gradient ascent)
  • each iteration computes $P(c^{(j)} \mid x^{(j)})$ for all $j$, and each possible $c^{(j)}$
  • this can be time-consuming, especially if there are a large number of classes and/or thousands of features to extract from each training sample.

7 February 2020

Sequence Labelling (Tagging)

• It is often the first step towards any syntactic analysis (which in turn, is often useful for semantic analysis).

• Named Entity Recognition labels words as belonging to persons, organisations, locations, or none of the above

  • Barack/PER Obama/PER spoke/NON from/NON the/NON White/LOC House/LOC today/NON ./NON

• Information Field Segmentation given specific type of text (classified advert, bibliography entry, etc.), identify which words belong to which “fields” (price/size/location, author/title/year)

  • 3BR/SIZE flat/TYPE in/NON Bruntsfield/LOC ,/NON near/LOC main/LOC roads/LOC ./NON Bright/FEAT well/FEAT maintained/FEAT …

• In sequence labelling, deciding the correct label depends on

  • the word to be labeled
  • the labels of surrounding words
  • Hidden Markov Model combines these sources of information probabilistically.

Parts of Speech

• Open-Class Words (or Content Words)

  • nouns, verbs, adjectives, adverbs
  • mostly content-bearing: they refer to objects, actions, and features in the world
  • open class, since there is no limit to what these words are, new ones are added all the time! (selfie, Brexit, ombishambles)

• Closed-Class Words (or Function Words)

  • pronouns, determiners, prepositions, connectives

  • there a limited number of these

  • mostly functional: to tie the concepts of a sentence together

  • new ones are rare:

    • so far none of the attempts to introduce new gender-neutral pronouns have gotten much traction

• The number of parts of speech (tags) to have is a both linguistic and also a practical consideration.

  • Do you want to distinguish between proper nouns (names) and common nouns?
  • Singular and plural nouns?
  • Past and present tense verbs?
  • etc.
  • Commonly used tagsets for English usually have 40-100 tags. E.g. Penn Treebank has 45.

• Morphologically rich (e.g. Turkish) languages often have compound morphosyntactic tags: Noun+A3sg+P2sg+Nom

  • Hundreds or thousands of possible combinations!
  • Predicting these requires more complex methods than what we will discuss.

PoS Tagging

• The problem of finding the best tag sequence for a sentence is also called decoding.

• PoS tagging is hard because:

  • Ambiguity

    • glass of water/NOUN vs. water/VERB the plants
    • wind/VERB down vs. a mighty wind/NOUN (homographs)

  • Sparse Data

    • Words we haven’t seen before (at all, or in this context)
    • Word-Tag pairs we haven’t seen before (e.g. if we verb a noun)

• Relevant knowledge for PoS tagging

  • The word itself

    • Some words may only be nouns, e.g. arrow
    • Some words are ambiguous, e.g. like, flies
    • Probabilities may help, if one tag is more likely than another

  • Tags of surrounding words

    • two determiners rarely follow each other
    • two base form verbs rarely follow each other
    • a determiner is almost always followed by an adjective or a noun

A Probabilistic Model for Tagging

1. Choose a tag conditioned on previous tag

   • Transition probability

2. Choose a word conditioned on its tag

   • Emission probability

     • Because every state emits a word (except <s> and </s>).

• So the model assumes

  • Each tag depends only on previous tag: a bigram (or n-gram) tag model
  • Words are independent given a tag

• Transition Probability Table

  

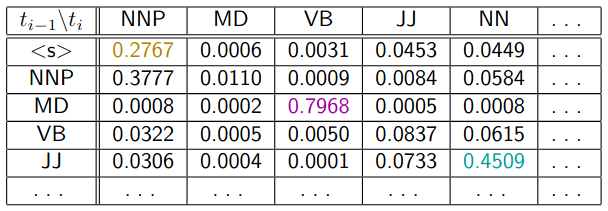
  • Leftmost column is the previous tag
  • Topmost row is the “next” tag
  • Every row should sum up to 1.

• Emission Probability Table

  

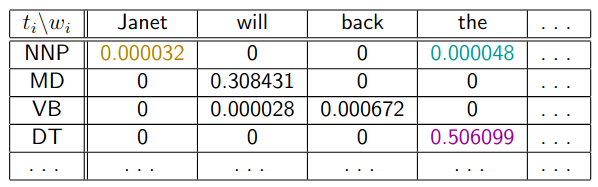
  • Leftmost column is the current tag
  • Topmost column is the emitted word
  • Every row should sum up to 1.

• In this model, joint probability $P(S, T) = \prod^n_{i=1} P(t_i \mid t_{i-1}) P(w_i \mid t_i)$

  • A product of transmission and emission probabilities for each word.

Actual Tagging with Hidden Markov Models (HMM)

• Given a sequence of words, what is the most probable state path that generated them?

• HMMs are quite similar to what we have seen earlier:

  • N-gram Model a model for sequences that also makes a Markov assumption but has no hidden variables
  • Navies Bayes a model with hidden variables (the classes) but no sequential dependencies
  • HMM a model for sequences with hidden variables

• Find the best tag sequence $T$ for an untagged sentence $S$: $\arg\max_T P(T \mid S)$

  • By Bayes’ Rule: $\arg\max_T P(T \mid S) = \arg\max_T P(S \mid T) P(T)$

    • and $P(S \mid T)P(T) = P(S, T)$ wooow!

• Brute-force enumeration of all the possible tag sequences takes $O(c^n)$ time for $c$ possible tags and $n$ words in the sentence.

The Viterbi Algorithm

• Dynamic programming algorithm to memorise smaller sub-problems to save time in return of space to avoid recomputation.
• We’ll see tomorrow.

11 February 2020

Viterbi Table

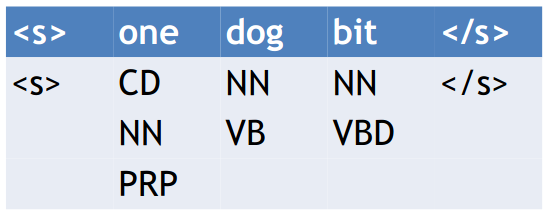
• The topmost row is the word sequence.

• The cells below are the PoS tags.

• You know Viterbi… Not gonna dwell into it again.

• Intuition: the best path of length $t$ ending in state $q$ must include the best path of length $t-1$ to the previous state. So:

  • Find the best path of length $t-1$ to each state

  • Consider extending each of those by 1 step, until state $q$

  • Take the best of those options as the best path to state $q$

  • And of course use a chart to store partial results as we go.

    • And use backtrace to construct the path.

      

• We can add up all probabilities in the last column to get the likelihood of (the probability of the entire) sequence.

• As probabilities can get really tiny quickly, thus risking underflow, we use costs instead.

  • Hence take minimum over sum of costs, instead of maximum over product of probabilities.

• We can use expectation-maximisation to “bootstrap” an HMM in an unsupervised fashion.

14 February 2020

Meta lecture. About evaluation mostly and doing NLP in practise.

Annotation

• Annotation costs time and money, you need to decide on

  • Source Data genre? size? licensing?
  • Annotation Scheme complexity? guidelines?
  • Annotators expertise? training?
  • Annotation Software graphical interface? scanning papers?
  • Quality Control multiple annotation? adjudication process?

• Text might be ambiguous

• There may be grey area between categories in the annotation scheme

  • Multiple equally valid decisions can be plausible

Inter-Annotator Agreement (IAA)

• An important way to estimate the reliability of annotations is to have multiple people independently annotate a common sample, and measure inter-annotator agreement.

  • Raw agreement rate is the proportion of labels in agreement.

    • Some measures take knowledge about the annotation scheme into account (e.g. counting singular vs plural noun as a minor disagreement compared to noun vs preposition).

• The agreement rate can be thought of as an upper bound (human ceiling) on the accuracy of a system evaluated on that dataset.

Cross-Validation

• What if our dataset is too small to have a nice train/test or train/dev/test split?

• $\textbf{k}$-fold cross validation: partition the data into $k$ pieces and treat them as mini held-out sets. Each fold is an experiment with a different held-out set, using the rest of the data for training.

  • After $k$ folds, every data point will have a held-out prediction.
  • If we are tuning the system via cross-validation, it is still important to have a separate blind test set.

Measuring a Model’s Performance

• Precision proportion of model’s answers that are right

• Recall proportion of test data that model gets right

• Bora: It is hard to differentiate… Precision seems to be much more common.

• 

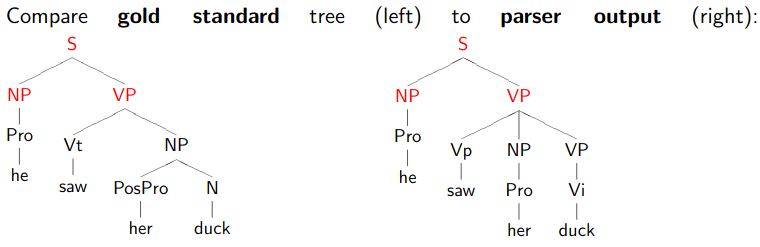
  • Pre-terminals (lexical categories) don’t count as constituents.
  • Precision: 3/5
  • Recall: 3/4

Bounds

• Upper Bounds

  • Turing Test

    • When using a human Gold Standard, check the agreement of humans against that standard.

• Lower Bounds

  • Baseline

    • Performance of a simpler model

  • Majority Baseline

    • Model always picks the most frequent/likely class.

Significance

• When we are evaluating a model against each other or to a bound, how do we decide if the differences we find are significant?

• In other words, should we interpret the differences as down to pure chance? Or is something more going on?

• Parametric when the underlying distribution is normal

  • t-test, z-test, …

• Non-parametric otherwise

  • Usually do need non-parametric tests: remembers Zipf’s Law!
  • Can use McNemar’s test or variants of it.

25 February 2020

• We have seen various ways to model word behaviour

  • Bag-of-words models ignore word order entirely
  • N-gram models capture a fixed-length history to predict word sequences
  • HMMs also capture fixed-length history, but also using latent variables
  • These are useful for various tasks, but a really accurate model of language needs more than a fixed-length history!

• There are often long-range dependencies!

  • The form of one word often depend on (or agrees with) another, even when arbitrarily many words intervene:

    • Sam/Dogs sleeps/sleep soundly.
    • Sam, who is my cousin, sleeps soundly.
    • Sam, the man with red hair who is my cousin, sleeps soundly.

  • We want models that can capture these dependencies: for translation, or for understanding.

• We may also want to capture substitutability at the phrasal level.

  • POS categories indicate which words are substitutable. For example, substituting adjectives:

    • I saw a red cat.
    • I saw a former cat.

  • Phrasal categories indicate which phrases are substitutable. For example, substituting a noun phrases:

    • Dogs sleep soundly.
    • My next-door neighbours sleep soundly.

Theories of Syntax

• A theory of syntax should explain which sentences are well-formed (grammatical) and which are not.

  • Note that well-formed is distinct from meaningful.

    • Famous example from Chomsky: Colorless green ideas sleep furiously.

  • However, we’ll see shortly that the reason we care about syntax is mainly for interpreting meaning.

• Context-Free Grammar (CFG) in today’s lecture

• Dependency Grammar following lecture

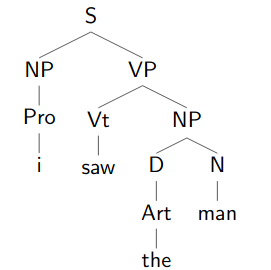
Context-Free Grammar

• Two types of grammar symbols:

  • terminals words
  • non-terminals phrasal categories like S, NP, VP, PP, etc with S being the start symbol

• Rules of the form $\text{Non-Terminal} \to \beta$ where $\beta$ is any string of non-terminals and terminals

• A CFG in Chomsky Normal Form only has rules of the form

  • $\text{NT} \to \text{NT}\ \text{NT}$
  • $\text{NT} \to t$

• To show that a sentence is well-formed under this CFG, we must provide a parse. One way to do this is by drawing a tree.

  

Ambiguity

Structural Ambiguity

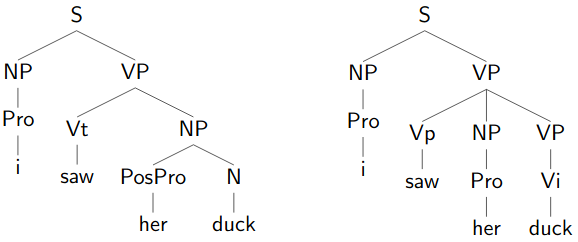
• Some sentences have more than one parse.

• Here, the structural ambiguity is caused by POS ambiguity in several of the words.

  • Both are types of syntactic ambiguity.

Attachment Ambiguity

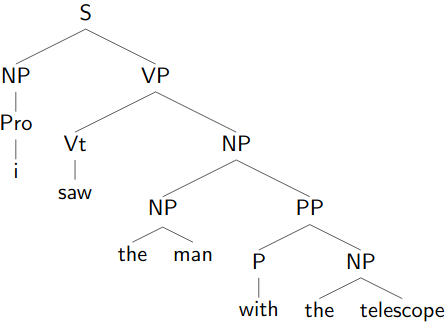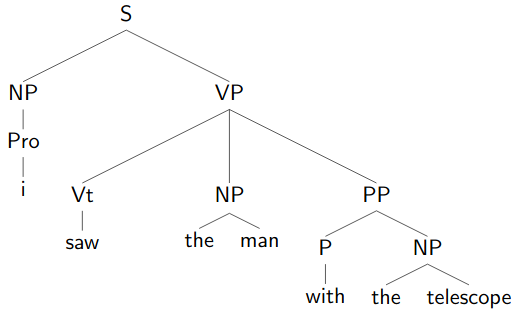“the man with the telescope”	“with the telescope I saw the man

• Some sentences have structural ambiguity even without PoS ambiguity. This is called attachment ambiguity.

• Depends on where different phrases attach in the tree.

• Different attachments often have different meanings:

  • I saw the man with the telescope.
  • She ate the pizza on the floor.
  • Good boys and girls get presents from Santa.

Parse Trees

• We want to use parse trees as scaffolding for semantics

  • Compositional Semantics

    • The meaning of a constituent is a function of the meaning of its children.
    • Bora: The meaning of a whole comes from its children…

  • Rule-To-Rule Semantics

    • That function is determined by the rule which licenses the constituent.
    • Bora: …and the way they are combined in the whole.

• So ambiguity matters a lot!

Parsing

• Computing the structure(s) for an input string given a grammar.

  • Recognizers are those that tells us whether the sentence has a valid parse, but not what the parse is.

• As usual, ambiguity is a huge problem

  • For correctness need to find the right structure to get the right meaning
  • For efficiency searching all possible structures can be very slow

• Global Ambiguity

  • Multiple analyses for a full sentence.
  • E.g. “I saw the man with the telescope.”

• Local Ambiguity

  • Multiple analyses for parts of sentence.

  • E.g. “The dog bit the child.”

    • First three words could be NP (but aren’t).
    • Building useless partial structures wastes time.
    • Avoiding useless computation is a major issue in parsing.

• Syntactic ambiguity is rampant; humans don’t even notice because we are good at using context/semantics to disambiguate.

• All parsers have two fundamental properties:

  • Directionality the sequence in which the structures are constructed

    • Top-Down start with root category (S), choose expansions, build down to words
    • Bottom-Up build subtrees over words, build up to (S)
    • Mixed strategies are also possible (e.g. left corner parsers)

  • Search strategy the order in which the search space of possible analyses is explored

    • Depth-First Search

      • requires backtracking

      • very efficient for unambiguous structures

      • can be massively inefficient (exponential in sentence length) if faced with local ambiguity

        • blind backtracking may require re-building the same structure over and over: so, simple depth-first parsers are not used in NLP

    • Breadth-First Search

      • has higher memory requirements

    • Best-First Search

      • requires scoring each partial parse and purse the highest-scoring options first

Recursive Descent Parsing

• Top-down, depth-first.
• You know it by heart from Compiling Techniques, skipping.

Shift-Reduce Parsing

• Bottom-up, depth-first.

• Repeatedly

  • Whenever possible, reduce one or more items from top of stack that match RHS of rule, replacing with LHS of rule
  • When that is not possible, shift an input symbol onto a stack
  • Otherwise, backtrack

28 February 2020

CKY Parsing

• CKY (Cocke, Kasami, Younger) is a bottom-up, breadth-first parsing algorithm.

• Original version assumes grammar in Chomsky Normal Form.

• Dynamic (chart) programming algorithm.

  • Add constituent $A$ in cell $(i, j)$ if there is:

    • a rule $A\to B$, and a $B$ in cell $(i, j)$, or
    • a rule $A \to B\ C$, and a $B$ in cell $(i, k)$ and a $C$ in cell $(k, j)$
    • it will be quite obvious in a minute on the table

• Fills chart in order

  • Only looks for rules that use a constituent of length $n$ after finding all constituents of length less than $n$.
  • So, guaranteed to find all possible parses.

• Takes time $O(Gn^3)$, where $G$ is the number of grammar rules and $n$ is the number of words in the sentence.

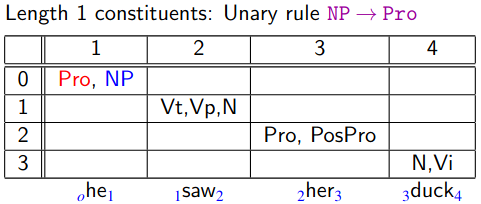
Step by Step

1. 

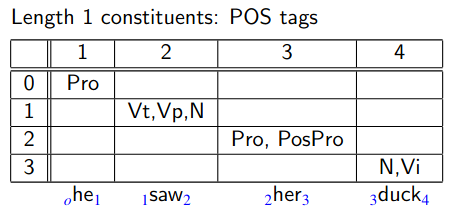
   • We have added all PoS tags that are allowed for each word.

   • Beware that the bottom-left half of the table (excluding the diagonal) is empty.

     • We are interested in cells $(x, y)$ where $x \le y$.

2. 

   • Red shows which children create which parents.

     • Normally we add pointers from parent to child to store this info permanently, but here we omit them for clarity.

3. 

   • More unary rule construction.

4. 

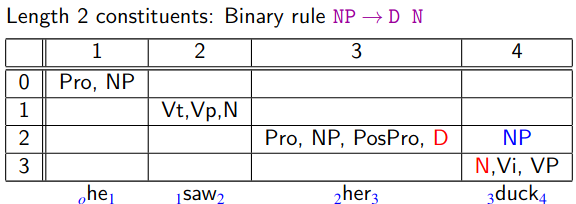
   • A-ha, this is interesting!
   • Given binary rule $\text{NP} \to \text{D}\ \text{N}$, we construct $\text{NP}$ in cell $(2,4)$ from $\text{D}$ in cell $(2, 3)$ and from $\text{N}$ in cell $(3,4)$.

5. Skipping intermediate steps…

   • Remember that, say for cell $(1, 4)$ we consider all of the following:

     • $(1, 2)$ and $(2, 4)$
     • $(1, 3)$ and $(3, 4)$

   • In general, for cell $(x, y)$ [remembering that $x$ is always less than $y$] you should consider all of the following:

     • $(x, x+1)$ and $(x+1, y)$
     • $(x, x+2)$ and $(x+2, y)$
     • …
     • $(x, y-1)$ and $(y-1, y)$

6. 

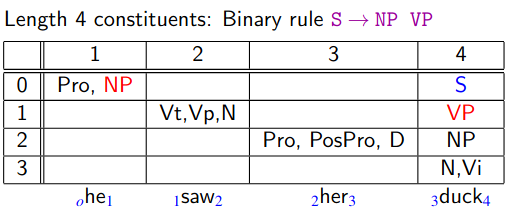
   • The top-right cell contains the root of the parse tree, which then can be constructed using backpointers.

CKY Ordering

• We filled in all short entries, then longer ones.

• Effectively, we are sweeping out diagonals beginning with the main diagonal and moving up to the right.

  • Other orders can work too, but it’s always shorter first!

CKY in Practise

• Avoids re-computing substructures so much more efficient than depth-first parsers in worst case.

  • E.g. with natural languages. Where ambiguity is none or extremely limited (e.g. formal languages), depth-first parsers can be extremely efficient!

• Still may compute a lot of unnecessary partial parses.

• Simple version requires converting the grammar to Chomsky Normal Formal.

  • May cause blowup! Remember that CKY is $O(Gn^3)$.

• Various other chart parsing methods avoid these issues by combining top-down and bottom-up approaches.

  • But rather, we will focus statistical parsing which can help deal with both ambiguity and efficiency issues.

Treebank Grammars

• The big idea: instead of paying linguists to write a grammar, pay them to annotate real sentences with parse trees.

• This way, we implicitly get a grammar (for CFG: read the rules off the trees)

• And we get probabilities for those rules (using any of our fav estimation techniques).

  • We can use these probabilities to improve disambiguation and even speed up parsing.

Probabilistic Context Free Grammars (PCFG)

• A probabilistic context free grammar (PCFG) is a CFG where each rule $\text{NT} \to \beta$ (where $\beta$ is a symbol sequence) is assigned a probability $P(\beta\mid \text{NT})$.

• The sum over all expansions of $\text{NT}$ must be equal to 1. $\sum_{\beta'} P(\beta' \mid \text{NT}) = 1$

• Easiest way to create a PCFG from a tree: MLE

  • Count all occurrences of $\text{NT} \to \beta$ in the treebank
  • Divide by the count of all rules whose LHS is $\text{NT}$to get $P(\beta\mid \text{NT})$
  • But as usual, many rules have very low frequencies, so MLE isn’t good enough and we need to smooth.

• Under this model, the probability of a parse $t$ is simply the product of all rules in the parse: $P(t) = \prod_{\text{NT} \to \beta\ \in\ t} P(\text{NT} \to \beta)$

• Given multiple trees for a sentence, choose the one with the highest probability (or lowest cost).

  • This is regarding global ambiguity.

• Probability of a sentence is the sum of the probabilities over all the parses.

Probabilistic CYK

• Goal: return the highest probability parse of the sentence (analogous to Viterbi)

  • When we find an NT spanning $(i,j)$, store its probability along with its label in cell $(i,j)$
  • If we later find an NT with the same span but higher probability, replace the probability and the backpointers for NT in cell $(i,j)$

• Inside algorithm computes the probability of the whole sentence (analogous to forward algorithm).

• Inside-outside algorithm is a form of EM that learns grammar rule probabilities from unannotated sentences (analogous to forward-backward).

• Exhaustive parsing can be really expensive.

  • Best-first parsing can help!

Best-First Probabilistic Parsing

• Basic idea: use probabilities of subtrees to decide which ones to build up further.

  • Each time we find a new constituent, we give it a score (“figure of merit”) and add it to an agenda, which is ordered by score.
  • Then we pop the next item off the agenda, add it to the chart, and see which new constituents we can make using it.
  • We add those to the agenda, and iterate.

• Notice we are no longer filling the chart in any fixed order!

• Often limiting the size of the agenda by prunning out low-scoring edges (beam search).

• Not as great as you might first think!

  • 

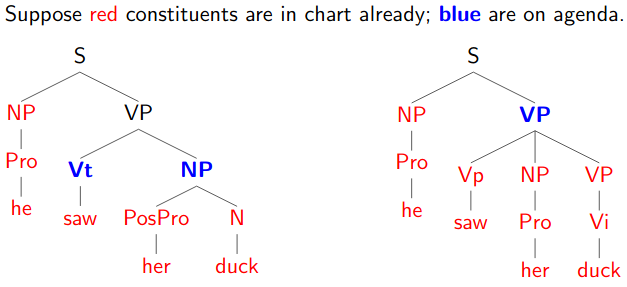
  • Because higher on the tree, lower is the probability so in the majority of the cases, you will expand all the lower constituents before moving up.

    • If we use raw probabilities for the score, smaller constituents will almost always have higher scores.

      • Meaning we pop all the small constituents off the agenda before the larger ones.
      • Which would be very much like exhaustive bottom-up parsing!

    • Instead, we can divide by the number of words in the constituent.

      • Very much like we did when comparing language models (recall per-word cross-entropy).

    • This works much better, but now not guaranteed to find the best parse first.

Lexical Dependencies

• Replacing one word with another with the same POS will never result in a different parsing decision, even though it should!

  • Examples:

    • She stood by the door covered in tears vs. She stood by the door covered in ivy

  • But PCFGs are context-free, so an NP is an NP, and will have the same expansion probabilities regardless of where it appears.

3 March 2020

Evaluating Parse Accuracy

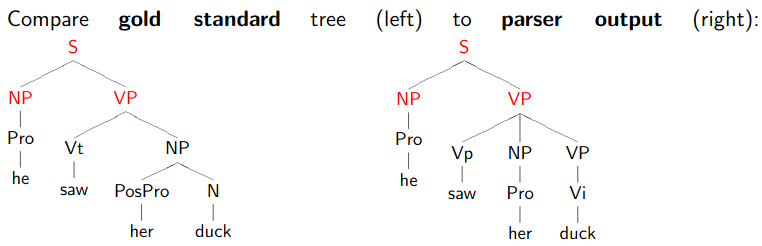
• Output constituent is counted correct if there is a gold constituent that spans the same sentence positions.
• Pre-terminals (lexical categories) don’t count as constituents.

Handling Lexical Dependencies (Lexicalisation)

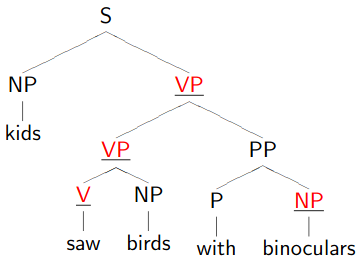
• Replacing one word with another with the same PoS will never result in a different parsing decision, even though it should!

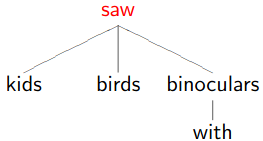
  • kids saw birds with fish vs. kids saw birds with binoculars

• Lexicalisation: create new categories, by adding the lexical head of the phrase.

  • For example:

    

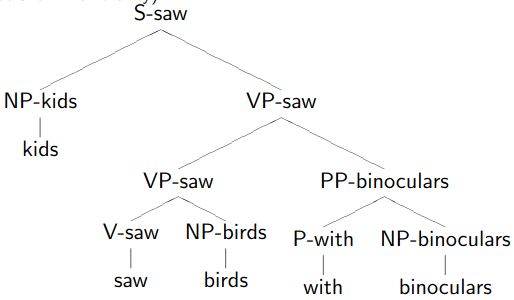
    • Now consider: $\text{VP - saw} \to \text{VP - saw } \text{ PP - fish}$ vs. $\text{VP - saw} \to \text{VP - saw } \text{ PP - binoculars}$

• Practical Issues

  • Identifying the head of every rule is not always straightforward.

  • All this category-splitting makes the grammar much more specific (good!)

    • But leads to huge grammar blowup and very sparse data (bad!)

  • Do we really need phrase structure in the first place? Not always!

    • Today: syntax (and parsing) without constituent structure

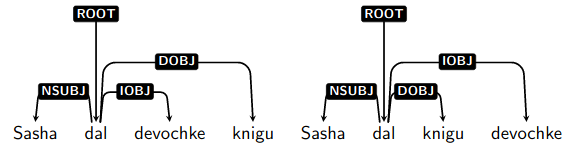
Dependency Trees

1.

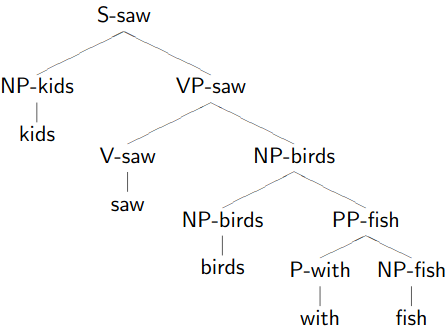
2. Remove phrasal categories

   

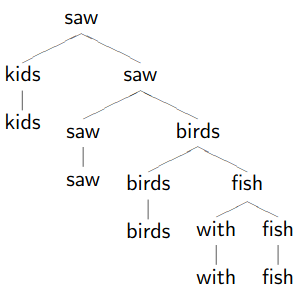
3. Remove duplicated terminals

   

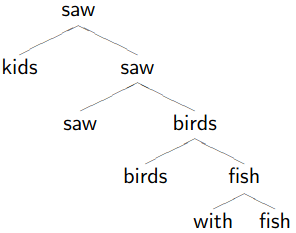
4. Collapse chains of duplicates -

   -

   

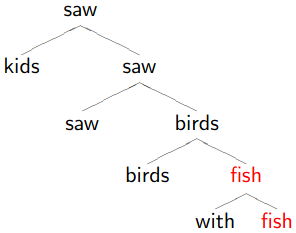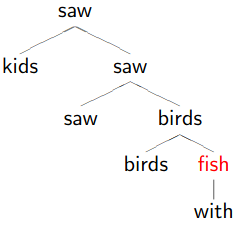
5. Result

   

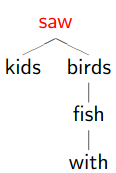
• Don’t worry if the tree looks stupid to you, because it is!

  • This demonstrates how dependency trees can help with correct parsing too.

  • The right one is

    

• Meaning of words within a sentence depend on one another, mostly in asymmetric, binary relations.

  • Though some constructions don’t cleanly fit this pattern: e.g. coordination & relative clauses.

• Also, in languages with free word order (e.g. Turkish, Russian), phrase structure (constituency) grammars don’t make as much sense.

  • E.g. we would need both $\text{S} \to \text{NP } \text{VP}$ and $\text S \to \text {VP } \text { NP}$. Not very informative about what is really going on.

  • In contrast, dependency relations stay constant:

    

• Edge labels can help us distinguish different kinds of head $\to$ modifier relations:

  

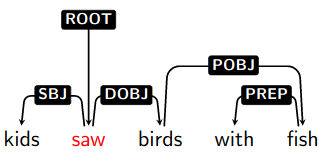
  • Important relations for English include subject, direct object, determiner, adjective, modifier, adverbial modifier, …

• A sentence’s dependency parse is said to be projective if every subtree (node and all its descendants) occupies a contiguous span of the sentence:

  

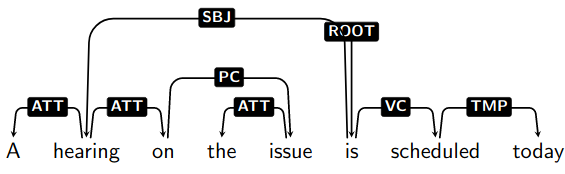
  • In which case, the dependency parse can be drawn on top of the sentence without any crossing edges.
  • Nonprojectivity is rare in English but quite common in many other languages.

Head Rules

• How can we find each phrase’s head in the first place?

• The standard solution is to use head rules

  • For every non-unary (P)CFG production, designate on RHS non-terminal as containing the head.

  • E.g. $\text S \to \text{NP } \underline{ VP}$

    

  • We can also employ heuristics to scale this to large grammars: within an NP, last immediate N child is the head

Pros and Cons

Pros

• Sensible framework for free word order languages

• Identifies syntactic relations directly.

  • Using CFG, how would you identify the subject of a sentence?

• Dependency pairs/chains can make good features in classifiers, information-extractors, etc.

• Parsers can be very fast!

Cons

• The assumption of asymmetric binary relations isn’t always right…

  • E.g. how to parse dogs and cats

Direct Dependency Parsing

• CKY can be adapted, though efficiency is a concern: obvious approach is $O(Gn^5)$; Eisner algorithm brings it back down to $O(Gn^3)$
• Shift-reduce is more efficient, and doesn’t even require a grammar!

Shift-Reduce Parsing

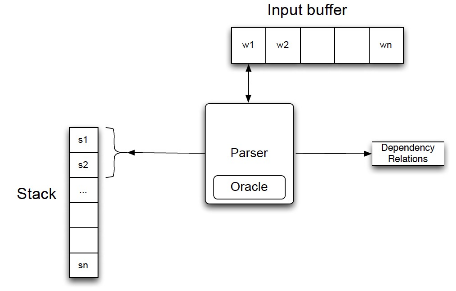
• 3 possible actions:

  1. LeftArc assign head-dependent relation between $s1$ and $s2$; pop $s2$
  2. RightArc assign head-dependent relation between $s2$ and $s1$; pop $s1$
  3. Shift put $w1$ on top of the stack

• Remember, dependency relations point from head to dependent.

• Both LeftArc and RightArc leave the head at the top of the stack!

Transition-Based Parsing

• Latent structure is just edges between words.
• Train a classifier as the oracle to predict next action (Shift, LeftArc, RightArc), and proceed left-to-right through the sentence.
• $O(n)$ time complexity!
• Only finds projective trees (without special extensions)

Graph-Based Parsing

• From a fully connected directed graph of all possible edges, choose the best ones that form a tree.

• Edge-factored models:

  • classifier assigns a non-negative score to each possible edge
  • maximum spanning tree algorithm finds the spanning tree with the highest total score in $O(n^2)$ time

• Can be formulated as constraint-satisfaction problem with integer linear programming

Comparison

• Transition-Based

  • Scoring function can look at any part of the stack
  • No optimality guarantees for search
  • Linear-time
  • (Classically) Projective only

• Graph-Based

  • Scoring function limited by factorisation
  • Optimal search within the model
  • Quadratic time
  • No projectivity constraint

• Conversion-Based

  • In terms of accuracy, sometimes best to first constituency-parse, then convert to dependencies
  • Slower than direct methods
  • You need grammar and head rules

• Shift-Reduce

  • Bora: ???

6 March 2020

Meaning

• One grand goal of artificial intelligence is to understand what people mean when they talk.

• But how do we know if we succeeded?

• Meaning and understanding can lead to deep “philosophical” questions.

• NLP usually takes a more pragmatic view: can the computer behave as though it understands (in order to do what we want)

  • Dialogue systems (e.g. Eliza)
  • Machine translation
  • Question answering

• What issues will we face in building such systems?

Question Answering

• We would like to build

  • a machine that answers questions in natural language
  • may have access to knowledge bases
  • may have access to vast quantities of English text

• Basically, a smarter Google

• This is typically called Question Answering

Semantics

• To build our QA system, we will need to deal with issues in semantics, i.e. meaning

• Lexical Semantics: the meanings of individual words

• Sentential Semantics: how word meanings combine (after that in a sentence)

  • Who did what to whom, when, how, why…

• Some examples to highlight problems in lexical semantics:

  • plant (flora) vs plant (infrastructure)

    • Words may have different meanings (senses).
    • We need to be able to disambiguate between them.

  • vacation and holiday

    • Words may have the same meaning (synonyms).
    • We need to be able to match them.

  • animals and polar bears

    • Words can refer to a subset (hyponym) or superset (hypernym) of the concept referred to by another word.
    • We need to have a database of such A is-a B relationships, called ontology.

  • remove vs eliminate

    • Words may be related in other ways, including similarity and gradation.
    • We need to be able to recognise these to give appropriate responses.

  • Poland and Central Europe

    • We need to do inference.
    • A problem for sentential, not lexical, semantics.

• Some of these problems can be solved with a good ontology, e.g. WordNet.

  • WordNet is a hand-built resource containing 117k synsets: sets of synonymous words

  • Synsets are connected by relations such as

    • hyponym/hypernym (IS-A: chair-furniture)
    • meronym (PART-WHOLE: leg-chair)
    • antonym (OPPOSITES: good-bad)

• Words are typically semantically ambiguous.

  • But there’s a lot of regularity (and hence predictability) in the range of senses a word can take.
  • Those senses also influence the word’s syntactic behaviour.
  • Word senses can be productive, making a dictionary model (like WordNet) inadequate.

• Lumping vs Splitting

  • Lump usages of a word into small number of senses
  • Split senses to reflect fine-grained distinctions

• Another way to define senses is to look if occurrences of the word have different translations.

  • Eng. Interest $\to$ German

    • Zins: financial charge paid for load
    • Anteil: stake in a company
    • Interesse: all other sense

• Polysemous is a word having multiple senses.

Word Sense Disambiguation (WSD)

• For many applications, we would like to disambiguate senses

  • We may be only interested in one sense
  • Searching for chemical plant on the web, we do not want to know about chemicals in bananas.

• Task: given a sense ambiguous word, find the sense in a given context

• WSD as classification

  • Given a word token in context, which sense (class) does it belong to?

  • We can train a supervised classifier, assuming sense-labelled training data

  • Lots of options available:

    • Naive Bayes, Maximum Entropy
    • Decision Lists
    • Decision Trees

• Issues with WSD

  • Not always clear how fine-grained the gold-standard should be

  • Difficult/expensive to annotate corpora with fine-grained senses

  • Classifiers must be trained separately for each word

    • Hard to learn anything for infrequent or unseen words
    • Requires new annotations for each new word

Semantic Classes

• Other approaches, such as named entity recognition and supersense tagging define coarse-grained semantic categories like person, location, artifact
• Like sense, can disambiguate: Apple as organisation vs food
• Unlike senses, which are refinements of particular words, classes are typically larger groupings.
• Unlike senses, classes can be applied to words/names not listen in a lexicon.

Named Entity Recognition (NER)

• Recognising and classifying proper names in text is important for many applications. A kind of information extraction.

• Different inventories of classes:

  • Smaller person, organisation, location, miscellaneous
  • Larger also product, work_of_art, historical_event, etc. as well as numeric value types (time, money, etc.)

• NER systems typically use some form of feature-based sequence tagging, with features like capitalisation being important.

• Lists of known names called gazetteers are also important.

Supersense Tagging

• Supersense tagging does beyond NER to cover all nouns and verbs.

10 March 2020

Word Similarity

• How to know if words have similar meanings?

• Can we just use a thesaurus?

  • May not have a thesaurus in every language.
  • Even if we do, many words and phrases will be missing.

• Let’s try to compute similarity automatically.

• Meaning from Context(s)

  • “a bottle of raki is on the table”
  • “everybody likes raki”
  • “raki makes you drunk”
  • “we make raki out of grapes”

Distributional Hypothesis

• Perhaps we can infer meaning just by looking at the contexts a word occurs in!

• Perhaps meaning is the contexts a word occurs in (Wittgenstein!)

• Either way, similar contexts imply similar meanings

  • This idea is known as the distributional hypothesis

• Represent each word $w_i$ as a vector of its contexts

  • Distributional semantic models also called vector-space models

• Each dimension is a context word; = 1 if it co-occurs with $w_i$, otherwise 0.

• For example:

  

  • Real vectors would be far more sparse!

The Context

Questions

• What defines “context”?

  • What are the dimensions?
  • What counts as co-occurrence?

• How to weight the context words (boolean? counts? other?)

• How to measure similarity between vectors?

Defining the Context

• There are two kinds of co-occurrence between two words:

  • First-Order Co-Occurrence (syntagmatic association)

    • Typically nearby each other. wrote is a first-order associate of book

  • Second-Order Co-Occurrence (paradigmatic association)

    • Have similar neighbours wrote is second-order associate of said and remarked

• Usually ignore stopwords (function words and other very frequent/uninformative words)

• Usually use a large window around the target word (e.g. 100 words, maybe even whole document)

• But smaller windows allow for relations other than co-occurrence

  • E.g. dependency relation from parser

• All of these for semantic similarity

  • For syntactic similarity, use a small windows (1-3 words) and track only frequent words.

Weighing the Context Words

• Binary indicators are not very informative.

• Presumably more frequent co-occurrences matter more.

• Is frequency good enough?

  • Frequent (overall) words are expected to have high counts in the context vector.

    • Regardless of whether they occur more often with this word than with others.

• We want to know which words occur unusually often in the context of $w$: more than we’d expect by chance?

• Put another way, what collocations include $w$?

Pointwise Mutual Information (PMI)

$\text{PMI}(x, y) = \log_2 \dfrac{P(x, y)}{P(x)P(y)}$

• where

  • $P(x, y)$ is the actual probability of seeing words $x$ and $y$ together.
  • $P(x)P(y)$ is the predicted probability of seeing words $x$ and $y$ together, IF $x$ and $y$ are independent!

• PMI tells us how much more/less likely the cooccurrence is than if the words were independent.

• Problems

  • In practise, PMI is computed with counts (using MLE).
  • Therefore, it is over-sensitive to the chance co-occurrence of infrequent words.

Alternatives to PMI for Finding Collocations

• There a lot!

  • Student $t$-test
  • Pearson’s $\chi^2$ statistic
  • Dice coefficient
  • Likelihood ratio test (Dunning, 1993)
  • Lin association measure (Lin, 1998)
  • …

• Of those listed above, Dunning LR test probably most reliable for low counts.

  • However, which works best may depend on the downstream too.

Improving PMI

• Use Positive PMI (PPMI)

  • Change all negative PMI values to 0.
  • Because of infrequent words, not enough data to accurately determine negative PMI values.

• Introduce smoothing in PMI computation.

Similarity (again)

• Assume you have context vectors for two words $\vec v$ and $\vec w$

  • Vectors in high-dimensional space.
  • Containing PMI (or PPMI) values for all context words.

• Vectors seem to capture both syntactic and semantic information.

• So the question is, how to measure the “distance” between two vectors?

• Euclidean Distance

  • Doesn’t work well even if one dimension has an extreme value.

• Dot Product

  • Vectors are longer if they have higher values in each dimension.

  • So more frequent words have higher dot products. (BORA: I doubt this if we are using PMI values)

    • Dot product is generally larger for longer vectors, regardless of similarity.

  • But we don’t want a similarity metric that is too sensitive to word frequency.

• Normalised Dot Product

  • Normalise through dividing by the length of each vector $\vec v \cdot \vec w / \left(|\vec v||\vec w|\right)$

  • The normalised dot product is just the cosine of the angle between vectors!

    • Ranges from -1 (vectors pointing opposite directions) to 1 (same direction)

• Again, there are many other similarity measures

  • Jaccard measure
  • Dice measure
  • Jenson-Shannon divergence
  • etc.
  • Again, depends on the downstream too.

Evaluation of Similarity Computations

• Intrinsic evaluation is often a comparison to psycholinguistic data

  • Relatedness judgements
  • Word association

• Relatedness Judgements

  • E.g. on a scale of 1-10, how related are the following concepts:

    • Lemon and Truth 1/10
    • Lemon and Orange 10/10

  • But still a funny task.

  • Answers depend a lot on how the question is asked (e.g. related vs similar)

• Word Association

  • Upon seeing or hearing a word, say the first word that comes to mind.

  • Data collected from lots of people provides probabilities of each answer.

  • For example, for Lemon

    • 0.16 Orange
    • 0.11 Sour
    • 0.09 Tree
    • …

• Benchmarking

  • Human judgements provide a ranked list of related words/associations for each word $w$
  • Computer system provides a ranked list of most similar words to $w$
  • Compute the Spearman Rank Correlation between the lists (how well do the rankings match)

Compact Space

• So far our vectors have length $V$, the size of the vocabulary.
• Do we really need this many dimensions?
• Can we represent words in a smaller dimensional space that preserves the similarity relationships of the larger space?

Latent Semantic Analysis (LSA)

• One of the earliest methods for reducing dimensions while preserving similarity.
• Like Principal Component Analysis (PCA) except that we do not subtract off the means.
• LSA representations actually work better than originals for many tasks.

Neural Network Methods

• Recent methods for learning reduced-dimensional representations (now often called embeddings).
• Train a neural network to predict context words based on input word. Use hidden layer(s) as the input word’s vector representation.
• Deep mathematical similarities to LSA, but can be faster to train.

Compositionality

• One definition of collocations: non-compositional phrases:

  • White House not just a house that is white

• But a lot of language is compositional

  • red barn
  • wooden plank

• Can we capture compositionality in a vector space model?

  • More formally, compositionality implies some operator $\dot\times$ such that $\text{meaning}(w_1 w_2) = \text{meaning}(w_1) \dot\times \text{meaning}(w_2)$

• Current work investigates possible operators

  • addition
  • tensor product
  • non-linear operations learned by neural networks

• One problem: words like “not”

  • themselves more like operators than points in space!

13 March 2020

Semantic (Thematic) Roles

• Instead of focusing on syntax, consider semantic/thematic roles defined by each event.

• Argument Structure and Alterations

  • Mary opened the door The door opened
  • John slices bread with a knife This bread slices easily The knife slices cleanly
  • John gave a present to Mary John gave Mary a present

• syntax $\not=$ semantics

• The semantic roles played by different participants in the sentence are not trivially inferable from syntactical relations.

  • … though there are patterns!
  • The idea of semantic roles can be combined with other aspects of meaning (beyond this course).

• Commonly Used Thematic Roles

  • Agent The boy kicked his toy
  • Theme The boy kicked his toy
  • Experiencer The boy felt sad
  • Result The girl built a shelf with power tools
  • Instrument The girl built a shelf with power tools
  • Source She came from home
  • etc.

• Issues with thematic roles

  • No universally agreed-upon set of roles

  • Items with the same role (e.g. Instrument) may not behave quite the same

    • “Sandy opened the door with a key” $\to$ “The key opened the door”
    • “Sand ate the salad with a fork” $\to$ “The fork ate the salad” (?)

  • The two main NLP resources for thematic roles avoid these problems by defining very fine-grained roles.

• Semantic role labelling is identifying which words/phrases play which roles in an event.

  • Traditional pipeline:

    1. Either assume or compute syntactic parse and predicate senses
    2. Argument identification (deterministic): select the predicate’s argument phrases (by parsing the parse tree)
    3. Argument classification: select a role for each argument (wrt to the frame role for the predicate’s sense)

    • Problems:

      • Numbered roles (e.g. load.01.ARG1) are predicate specific (load.01) in PropBank.
      • FrameNet tries to generalise via verb classes, but less treebank data.

FrameNet

• Tries to capture relationships among word and phrase meanings by assigning them the same frame (and so captures paraphrases).

• ~ 1,000 frames represent scenarios.

  • Most are associated with lexical units (predicates) but some are phrases

• Frames are explained with textual descriptions and linguistic examples.

  • 

17 March 2020

Discourse Coherence

• Making sense of verbal actions

  • We assume action choice isn’t arbitrary (choice is informed by the context).
  • So we infer more than we see.
  • And may change these inferences as we see more!

• Representation

  • How should discourse coherence be represented formally and computationally?

• Construction

  • What inference processes, and what knowledge sources, are used when identifying coherence relations?

• Examples:

  • “John can open Bill’s safe.” “He knows the combination.”

    • If “He” is John: we infer explanation (“because”)
    • If “He” is Bill: we infer (at best) continuation (“and”) with a very vague topic

  • “John can open Bill’s safe.” “He should change the combination.”

    • If “He” is Bill: we infer result (“so”)
    • If “He” is John: we infer a weaker result?
    • Subjects are more likely antecedents, but not here!
    • Pronouns shall be interpreted in a way that maximises coherence, even if this conflicts with predictions from other knowledge sources!

• Word Meaning

  • “A: Did you buy the apartment?” “B: Yes, but we rented it. / No, but we rented it.”

• Bridging

  • “John took an engine from Avon to Dansville.” “He picked up a boxcar. / He also took a boxcar.”

• Implicit Agreement

  • “M (to K and S): Karen ‘N’ I’re having a fight,” “M (to K and S): after she went out with Keith and not me.” “K (to M and S): Wul Mark, you never asked me out.”

    • “Well” entails (implicit) agreement.

• Dishonesty

  • “P: Do you have any bank accounts in Swiss banks, Mr. Bronston?” “B: No, sir.” “P: Have you ever?” “B: The company had an account there for about six months, in Zurich.”

  • The last sentence is interpreted as an indirect answer, implying no (he did not have a personal bank account in Swiss banks ever)

  • His answer is literally true, but negative answer is false!

    • In fact, Bronston had once had a large personal bank account in Switzerland, where over a five year period he had deposited more than $180,000.

  • Supreme Court overrrules conviction for perjury.

    • Different ruling probable if Bronston had said “only”.

• Gesture

  • Coherence relations connect speech and gesture and sequences of gestures.

    • speech so that gesture
    • speech by gesture
    • speech and moreover gesture

SDRT: The Logical Form (LF) of Monologue

• Logical form consists of

  1. Set $A$ of labels $\pi_1, \pi_2, \ldots$

     • Each label stands for a segment of discourse

  2. A mapping $F$ from each label to a formula representing its content

  3. Vocabulary includes coherence relations; e.g. $\text{Elaboration}(\pi_1, \pi_2)$.

• Logical Forms and Coherence

  • Coherent discourse is a single segment of rhetorically connected subsegments.

  • More formally:

    • The partial order over $A$ induced by $F$ has a unique root.

Example

• Bits in red are specific values that go beyond content that’s revealed by linguistic form.

  • They are inferred via commonsense reasoning that’s used to construct a maximally coherent interpretation.

Bora’s Notice

• This is hard. Better not to dwell too much on it.
• Just fail those questions if it comes to it.